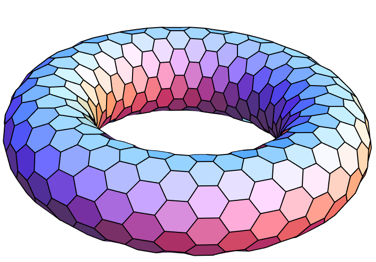
Periodic boundary conditions: the left & right edges of the grid are wrapped together, likewise for the top & bottom edges. This means that the hexagonal grid resides on the 2-dimensional surface of a 3-dimensional torus (donut).

STEP 1. Make a 2-dimensional grid (array) of "cells" which can each have a value of 0 (off/dead) or 1 (on/alive). Conway's famous "Game of Life" cellular automaton uses a square grid, but here we use a hexagonal grid (chicken-wire or honeycomb). Initialize the grid by filling it with all zeros. This is the "main grid".

STEP 2. Add a starting "seed" pattern to the main grid by changing some of the cell values to "1" (on/alive). Sometimes specific compact seeds are used, alternatively sometimes they are a random unstructured spread of ones that II call "primordial soup".

STEP 3. The program then looks at every cell in the entire main grid, one-by-one. When examining each cell, the total number of live neighbor cells is counted among its 6 immediately adjacent neighbor cells (if using "totalistic" rules). The program then consults the rule-set to decide if the central cell will be alive (1, on) or dead (0, off) in the next time-step. In order to not disturb the cell pattern that is being updating, all of these new values are accumulated on a separate "temporary grid".

STEP 4. After every cell is updated on the temporary grid, the main grid is re-initialized to all zeros, and then the temporary grid is copied to the main grid

STEP 5. Repeat Steps 3 & 4 for hundreds or thousands of iterations. The result of each iteration serves as the input for the next iteration. The grid is finite, so the live cell pattern will eventually go repeat or go extinct, although this could take thousands of time-steps.

Note: this "Hexagon-Multiverse" cellular automaton (HMCA) is similar to Conway's famous "Game of Life" (GOL) in the sense that both are 2-dimensional, have binary cell states, and are synchronous and deterministic. But the GOL uses a square grid, while the H-M CA uses a more natural (common in nature) and symmetrical hexagonal grid. More importantly, the HMCA achieves interesting results using a variety of different rule-sets, whereas the GOL is limited to a single rule-set.